Research:Wiki Participation Challenge Ernest Shackleton
About the Algorithm[edit]
Author: Keith T. Herring
Team Name: Ernest Shackleton
Source code: dumps.wikimedia.org
Ranking in Wikichallenge: 2nd
Dependencies[edit]
- Python
- Matlab
Files[edit]
- sample\construction.py (author Keith Herring): A python script for initializing the training samples from the data set of raw user edit histories. It initializes each sample as a time-limited record of a single user's edit history.
- feature\construction.py (author Keith Herring): A python script for converting the raw edit history of a time-limited user sample into the 206-element feature vector that the edits predictor operates on.
- random\forest (GPL licensed): Matlab CMEX implementation of the Breimann-Cutler Random Forest Regression Algorithm
- edits\learner.m (author Keith Herring): Matlab implemented algorithm for learning a suite of weak-to-strong future-edit models.
- ensemble\optimizer.m (author Keith Herring): Matlab implemented algorithm for finding the optimal model weights for the ensemble future edits predictor.
- edits\predictor.m (author Keith Herring): Matlab implemented algorithm that predicts the future edits for a user as a function of its associated edit-history derived 206-element feature vector.
- models.mat (author Keith Herring): Matlab data file containing the 34 decision tree models in the final ensemble.
- training\statistics.m at(author Keith Herring): Matlab data file containing the training population means and standard deviations for the 206 features.
- ensemble\weights.mat (author Keith Herring): Matlab data file containing the weights for the 34 models in the final ensemble.
Raw Data[edit]
An interesting aspect of this challenge was that it involved public data. As such there was opportunity to improve one's learning capability by obtaining additional data not included in the base data set (training.tsv). Given this setup, the first step of my solution was to write a web scraper for obtaining additional pre-Sept 1, 2010 (denoted in timestamp format 2010-09-01 in subsequent text) data for model training. More specifically I wanted to obtain a larger, more representative sample of user edit histories and also additional fields not included in the original training set. In total I gathered pre-2010-09-01 edit histories for approximately 1 million Wikipedia editors. The following attributes were scraped for each user:
- Blocked Timestamp: The timestamp in which a user was blocked. NULL if not blocked or blocked after Aug 31, 2010.
- Pre-2010-09-01 Edits: For each pre-2010-09-01 user-edit the following attributes were scraped:
- Edit ID
- Timestamp
- Article Title: The title of the article edited.
- Namespace: 0-5. All other namespaces were discarded, although an interesting extension would be to include the $>$ 5 namespaces to test if they provide useful information on the editing volume over lower namespaces.
- New Flag: Whether or not the edit created a new article
- Minor Flag: Whether or not the edit was marked as ``minor by the user.
- Comment Length: The length of the edit comment left by the user.
- Comment Auto Flag: Whether the comment was automatically generated. I defined this as comments that contained particular tags associated with several automated services, e.g. mw-redirect.
Namespace Classifier Bug[edit]
I noted during this scraping process a bug in the original training data. Specifically articles whose title started with a namespace keyword were incorrectly classified as being in that namespace, the regexp wasn't checking for the colon. The result being that some namespace 0-5 edits were being considered as namespace $>$ 5, and thus left out from the training set. I'm not sure if this bug was introduced during the construction of the archival dumps or the training set itself.
Training Set Construction[edit]
A single training sample can be constructed by considering a single user's edit history ending at any point before 2010-09-01. I used the following strategy for assembling a set of training samples from the raw data described above:
- Start at an initial end date of 153 days before 2010-09-01, i.e. April 1 2010.
- Create a sample from each user that has at least one edit during the year prior to the end date. This is to be consistent with the sampling strategy employed by wikipedia in constructing the base training set.
- Now move the end date back 30 days and repeat.
Repeating the above process for 32 offsets I obtained a training set with approximately 10 million samples, i.e. time-limited user edit histories.
Feature Construction[edit]
Given that a user's edit history is a multi-dimensional time-series over continuous time, it is necessary for tractability to project onto a lower-dimensional feature space, with the goal of retaining the relevant information in the time-series with respect to future editing behaviour. A priori my intuition was that many distinct features of a user's edit time series may play a role in influencing future edit behaviour. My strategy then was to construct a large number of features to feed into my learning algorithm to ensure most information would be available to the learning process. My final solution operated on the following features which I constructed from the raw edit data described above:
- Age: the number of days between a user's first edit and the end of the observation period (e.g. April 1, 2010=X for offset 0, X-30 days for offset 1, etc.). Both linear and log scale.
- Edits X: The number of edits per day made by the user over the last X days of the observation period. Log and linear scale. Calculated for X=1, 4 , 7 , 14, 28, 56, 112, 153, 365, 365*2, 365*4, 365*10 days.
- Norm Edits X: The number of edits made by the user over the last min(age,X) days. This normalizes for the fact that some users were not editing over the entire X day period.
- Exponential Edits X: The number of edits made by the user weighted by a decaying exponential with half life X days wrt the end of the observation period. This feature weights edits made more recently more heavily. Calculated for half lives: 1, 2, 4, 8, 16, 32, 40, 50, 64, 80, 90, 110, 120, 128, 256, 512, 1024 days.
- Norm Exponential Edits X: Same as above except normalized by the tail of the exponential before the user started editing.
- Duration X: The number of days between the Xth most recent edit made by the user and the end of the observation period. For users with less than X edits, it is set as a large constant. Calculated for X = 1, 2, 3, 4, 5, 8, 10, 13, 16, 20, 25, 28, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144 edits.
- 153 day time series: The number of edits made over 153 day intervals. Starting at the final 153 days of the observation period and progressing backwards in 30 day increments for 15 increments.
- Average Edit Time: The average edit timestamp (date and time) for the user.
- Standard Deviation Edit Time: The standard deviation (days) around the mean edit time.
- Sigma Edit Time: The number of standard deviations between the average edit time and the end of the observation period.
- Unique Articles: The percent of articles edited by the user which were unique, i.e. what fraction were distinct articles. Also the total raw number of distinct articles, number per age, and time windowed unique articles over the past 153 and 28 days.
- Namespace: For each of namespace 0-5, the percent of edits in that namespace. Also the total raw number, number per age, and time windowed number over the past 153 and 28 days.
- New Flag: The percent of edits in that were new/original. Also the total raw number, number per age, and time windowed number over the past 153 and 28 days.
- Minor Flag: The percent of edits in that were marked as minor. Also the total raw number, number per age, and time windowed number over the past 153 and 28 days.
- Comment: The percent of edits in that had a comment. Also the total raw number, number per age, and time windowed number over the past 153 and 28 days. Additionally the average comment length.
- Auto Flag: The percent of edits in that had auto-generated comments. Also the total raw number, number per age, and time windowed number over the past 153 and 28 days.
- Blocked Flag: Whether or not the user was blocked before the end of the observation period. April 1, 2010 or earlier for all training samples, August 31, 2010 or earlier for evaluation samples.
- Blocked Days: The number of days before the end of the observation period the user was blocked, if they were.
- Post Blocked Edits: The number of edits made by the user after they were blocked, but before the end of the observation period.
In total 206 features are used in the final model.
Sample Bias Correction[edit]
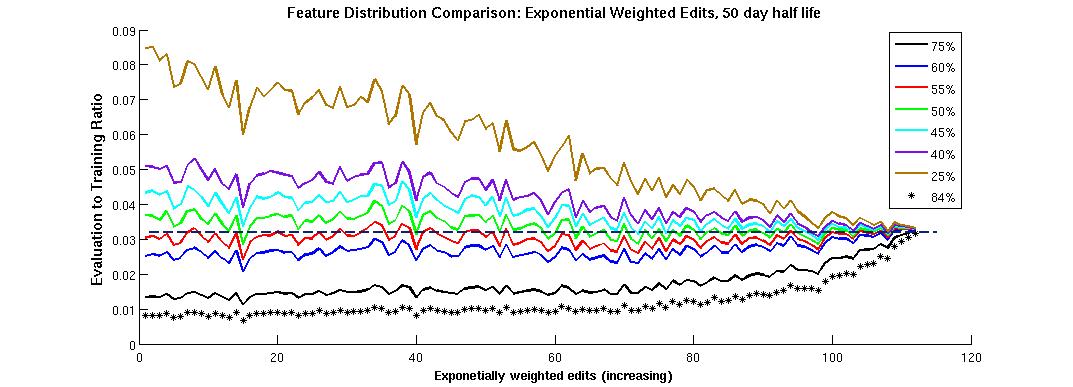
After calculating the features for both the training and evaluation sets, the latter referring to the 44514 users provided by the competition, I compared the feature distributions over the two sets. This analysis revealed nontrivial differences between the two sample distributions suggesting that the sample construction process I employed did not fully replicate the construction process used by the competition organizers. Figure 1 displays a comparison between the empirical distribution across the evaluation and training sets for two representative features. Each feature was binned into tens of value bins, such that the number of samples in each bin over each data set could be calculated. The x-axis of the figures represents the feature-bin, where increased index represents an increased feature value for the samples in that bin. They y-axis represents the number of evaluation set samples whose feature value is in the bin divided by the number of training set samples whose feature value is in the bin.
If the sample construction mechanisms for the evaluation and training sets were exactly the same, then the evaluation to training ratio would be approximately constant as a function of feature value bin, for all features. The *'ed curve corresponds to the empirically observed ratio for the original non-corrected training set as constructed according to the description above, i.e. random users selected such that they have at least one edit the year leading up to the end of the observation period. Here we see that the distribution ratio varies significantly (a factor 3-4) as a function of feature value. For example Figure 1b, which displays the total edits feature, shows that the training set has relatively more users who make a small number of edits over their observation period as compared to the evaluation set (about 100-1 ratio), while it has relatively fewer users who make a larger number of edits (about 25-1 ratio). This observation was consistent across features, e.g. the exponentially weighted edits feature in Figure 1a.
This observation suggests that the evaluation set was not constructed by uniformly selecting from the universe of users, but rather with some bias towards more active users. It should be noted then that the models submitted in this competition, by myself and others, will be trained/learned with respect to this active-user bias sample. If the Foundation wishes to have a model that operates on purely randomized users, with no such selection bias, then the chosen model(s) should be re-trained on a non-biased sample. However it may be the case that there was motivation for this active-user biased sampling strategy. I just want to point out that re-training may be a good idea depending on the Foundation's goals.
In order for the training set to be representative of the evaluation set population this active user bias had to be replicated. This can be done in many ways, e.g. unsupervised clustering in a subspace of the feature space. A more computationally tractable, yet generally less accurate, approach that I considered was to approach the bias from the output distribution of the training set. When the users were sampled uniformly I found that approximately 84 percent of them quit, i.e. had zero edits over their 153 day projection periods (note again these projection periods are all pre- Sept 1, 2010, since the latest (0 offset) begins April 1, 2010). The remaining training set output distribution ($>$ 0 future edits) died off exponentially (on log scale) at a slower subsequent rate. One way to inject active user bias into the training set then was to consider removing some fraction of the quitting users and observe how the feature distributions changed. The coloured curves show the feature distribution comparison as a function of having quitting users make up X percent of the training population, for X at values between 25 and 75 percent. Here I found that removing quitting users from the training set such that they made up somewhere between 40 and 60 percent of the population caused the (at least one dimensional) feature distributions to be approximately equivalent. The optimal percent X tough did vary by up to 10-20 percent depending on the feature, centred roughly at X = 50 percent across features. I used this correction method to reduce the bias between the training and evaluation sets. After bias correction I was left with approximately 2.5 million training samples. Not surprisingly it wasn't completely accurate as the observed model performance when applying cross-validation to the training set differed from the performance calculated by Kaggle on the evaluation set. This suggests that the two populations were still quite different, and that re-training my algorithm on the actual population of interest (be it fully randomized or the unknown competition method) will provide more representative results for that population.
Model Learning/Training[edit]
Given the high-dimensional feature space of the problem, I decided to use a custom variant of the random forest regression algorithm for learning a future edits prediction model.
Standard Random Forest Learning[edit]
The standard random forest regression algorithm proceeds as follows:
- Parameter Selection: Select some intuitive initial values for the random forest parameters. The main parameters of the random forest algorithm are as follows:
- Features per Node: The number of features to randomly choose from the feature universe at each node for making an optimal splitting decision at that node.
- Sample Size: The sample size (less than or equal to the fully available sample size) used to train each random decision tree.
- Maximum Leaf Size: Stopping condition on further node splitting. The lower this value, the more the tree overfits the data.
- T: The number of random decision trees to learn in the forest.
- Train: Train T random decision trees using the selected parameter values. For each tree record which samples were used to learn that tree in-bag (IB) vs those that were left out out-of-bag (OOB).
- OOB Validation: For each tree make predictions on all of its associated OOB samples. Form the overall prediction as the mean prediction across all T trees.
- Parameter Optimization: Repeat the above steps for new/tweaked parameter values until satisfied that a quasi-optimal set of parameters have been found.
Future Edits Learning Algorithm[edit]
The algorithm I wrote for learning future editing behaviour proceeds as follows:
- Random Parameter Random Trees: Rather than using the same parameter values across all trees in the forest, I instead constructed random decision trees one at a time. Each tree used random parameter values. In total approximately 3000 such trees were generated. The parameter values where randomly chosen for each tree independently as follows:
- Features per Node: Select a Weak, Medium, Strong learner with probabilities 65, 25, 10 percent respectively. Where:
- A weak learner has numfeatures randomly uniformly chosen between 1 and 10.
- A medium learner has numfeatures randomly uniformly chosen between 1 and 50.
- A strong learner has numfeatures randomly uniformly chosen between 1 and the total number of features (206).
- Sample Size: Randomly choose the sample size between 1 and 50 percent of the training data.
- Maximum Leaf Size: Randomly choose the maximum leaf size uniformly between Sample size divided by 50 (underfit extreme) and Sample size divided by 500000 (overfit extreme). With proper bounding between 1 and the samplesize - 1.I used an implementation of the Briemann Cutler algorithm (GPL licensed) for building the individual trees.
- Features per Node: Select a Weak, Medium, Strong learner with probabilities 65, 25, 10 percent respectively. Where:
- Ensemble Optimization: Rather than weighting each tree/model equally, as is done in the standard algorithm, my algorithm takes into account the second order performance statistics across models. Finding the optimal weights across models/trees can be formulated as the following quadratic optimization problem: where represents the ensemble weight of the tree/model, and is the covariance matrix of the model/tree errors . Using to weight the models in the ensemble takes into account the individual model performances and their correlation to one another, generally providing a better result.
- Calculating the Error Covariance Matrix: When calculating the error covariance matrix it is important to only use the OOB samples for each model, otherwise you would be overfitting the data. Since the OOB samples vary by model, the covariance between any two models must be calculated on the intersection of the OOB samples from both models. To ensure that the resulting covariance matrix is positive definite, and hence the quadratic optimization problem above has a unique solution (follows from the matrix being hermitian), it is important that the number of intersecting OOB samples be statistically significant. This is why I restricted the sample size to be at most 50 percent of the entire training sample for each tree. This ensures on average 25 percent of the data will be available for calculating the covariances for the most extreme models (those using 50 percent).
- Sequential Optimization: Since I learned thousands of models/trees, calculating the full error covariance matrix across all models is intractable. Instead I used the following heuristic for sequentially approximating the optimal weight vector
- Let denote the optimal weight vector at stage of the algorithm, i.e. after having processed models for
- Let denote the subset of models (out of the first ) that have non-negligible weight in the corresponding weight vector . Here I used the threshold of for classifying a weight as being negligible or not.
- At stage initialize recursively as follows: i.e. add the model to the current set of non-negligibly weighted models.
- Next solve for by using a quadratic solver for the quadratic optimization problem defined above using the error covariance matrix for the models in . Again the individual covariances are calculated on the intersection of the OOB samples for each model.
- Throw out any models in have negligible weight, i.e.
- Increment and repeat, stoping after . Using this heuristic I found that out of the approximately 3000 models, 34 had non-negligible weight, i.e. provided useful non-redundant prediction capability.
- Final Model Execution: The final future edits predictor routine then operates on an input as follows:
- Calculate the prediction for each of the final models , on the associated 206 element feature vector of the user under consideration.
- Calculate the final ensemble prediction as a weighted sum of the individual model predictions, using the calculated optimal weight vector.
Conclusions and Interpretation[edit]
Finally it is of most interest to understand which of the 206 features contained the most information wrt to predicting future editing behaviour. A measure of feature/variable's predictive capacity often used in decision trees is the permutation importance. The permutation importance of the feature is calculated on a given decision tree by first calculating the performance on the out-of-bag (OOB) samples. Next performance is calculated on the same OOB samples with their feature value randomly permuted. The importance of that variable/feature wrt the decision tree then is calculated as the difference between the two performance. A variable/feature with a large difference in performances signifies greater importance since the random permutation of that feature caused significant decrease in prediction performance.
The tables on the following pages rank the importances of the 206 features as averaged over the 34 trees in the ensemble predictor. Here we see that it was the timing and volume of a user's edits that played the most important role in predicting their future editing volume, i.e. exponentially weighted editing volumes. The attributes of the edits themselves, e.g. namespace, comments, etc played a lessor role. It should be noted that this importance measure is an aggregate measure. Features such as whether the user was blocked before the end of the observation period were quite informative as expected, however the percentage of blocked users is so small that its importance on the aggregate population prediction is also small.