Research:Post-edit feedback/PEF-1
| This page in a nutshell: The results from the first iteration of R:PEF indicate that post-edit feedback produces a marginal/insignificant increase in newbie contributions without negative side-effects on quality. Read a summary of the results on the Wikimedia blog. |
This page documents the results of the first iteration of the Post-edit feedback experiment. The goal of the experiment was to determine whether receiving feedback had any significant desirable or undesirable effect on the volume and quality of contributions by new registered users, compared to the control group.
We measured the effects on volume by analyzing the number of edits, contribution size and time to threshold for participants in each experimental condition; we measured the impact of the experiment on quality by looking at the rate of reverts and blocks in each experimental condition.
Prior to performing the analysis we generated a clean dataset from the entire population of participants in the experiment to filter out known outliers and focus on genuinely new registered users.
Unless otherwise noted, all analyses refer to a 2-week interval since registration time to include a supplementary week after the 1-week treatment period. We report when significant differences emerge comparing the in-treatment and post-treatment period.
Research questions[edit]
- RQ1. Does receiving feedback increase the number of edits?
- RQ2. Does feedback lead to larger contributions?
- RQ3. Does receiving feedback shorten the time to the second contribution?
- RQ4. Does feedback affect the rate at which newcomers are blocked?
- RQ5. Does feedback affect the success rate of newcomers?
Dataset[edit]
A total of 36,072 new registered users participated in this experiment, i.e. approximately 12K users per condition. 18,347 users in the sample were active, having clicked at least one time on the edit button.
As the focus of this experiment is on genuinely new registered users who received the treatment (which is triggered upon completing the first edit), we filtered from the sample all users matching the following criteria:
- attached users
- "attached users" are editors who previously registered an account on another wiki. They appear as "attached" to the English Wikipedia (locally registered for the first time on this wiki) upon their first login. We looked at the time difference between global registration dates and local registration dates on the English Wikipedia and considered attached users as genuine new users only if the registration date difference was smaller than the eligibility period (7 days). We found 427 users where the difference was greater than 7 days and that we filtered out from the sample.
- legitimate sockpuppets
- some users register legitimate alternate accounts for a variety of reasons. We want to filter out these editors as they are not genuinely new users. We found 3 users in the sample whose account was flagged as a legitimate alternate account.
- blocked users
- we removed from the sample all users who got blocked between their registration time and and the cut-off date of the present analysis (2012-09-05 00:00:00 UTC). We found 653 users blocked from the PEF1 sample.
- non-editing users
- out of the total population of eligible users, 8,975 completed an edit during the treatment period across all namespaces (6,473 edited the main Article namespace at least once). This gives 27,097 users who didn't complete any edit during the treatment period.
Applying the above filters, a clean dataset was generated of 8,571 users. The sample sizes for the separate treatments, where not listed explicitly, are those shown in the table below:
| Treatment | Sample Size |
|---|---|
| Control | 2931 |
| Confirmation | 2866 |
| Gratitude | 2815 |
Edit volume[edit]
Edit count[edit]
The following analysis address the question:
- RQ1. Does receiving feedback increase the number of edits?
Edit count is the most direct measure of editor activity. We measured the total edit counts of new editors that were added by experimental condition in the first 14 days of activity since registration. New users would not receive the treatment message until after completing their first edit. Therefore, for each editor included in the experiment the first contribution was omitted.
Table 2 gives the fraction of users that went on to make a second edit after receiving feedback:
| Treatment | Rate of second edits |
|---|---|
| Control | 42.37% |
| Confirmation | 43.72% |
| Gratitude | 41.14% |
Table 3 reports the mean edit count for each treatment:
| Treatment | Sample Size | Mean | Shapiro-Wilk Confidence | T-Test P-value against Control | |
|---|---|---|---|---|---|
| Control | 2884 | 4.805132 | 2.2e-16 | -- | |
| Confirmation | 2810 | 5.93274 | 2.2e-16 | 0.08938. | |
| Gratitude | 2761 | 5.931909 | 2.2e-16 | 0.05222. | |
| Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 | |||||
The distribution of edits per editor in the sample is skewed, the box plot in the figure above shows the edit count distribution per treatment on a log scale. Due to the skew in the data, we measured differences across treatments on the log transform of the edit count. Both experimental conditions displayed an increase of 23.5% in mean edit volume over the control. When comparing the "Confirmation" group against the control only marginal significance was observed. The edit count volume of the "Gratitude" condition outperformed the control with a significance level close to p=0.05. These results indicate that both types of feedback encourage a higher level of activity in new contributors.
Bytes added[edit]
This analysis focuses on addressing the following research question:
- RQ2: Does feedback lead to larger contributions?
The bytes added are computed in four ways for each editor:
- Net - the net sum of bytes added or removed
- Positive - the sum of bytes added
- Negative - the sum of bytes removed
Below are the means of byte changed normalized by edit count for each group. We considered logarithmic transformations of bytes changed to work with normally distributed data. In order to perform the log operation on the distribution over "Net" byte count the net negative samples were ommited (about 15% of total samples). The samples for total bytes added for any given editor were normalized by edit count, so for example, if an editor had made five edits contributing 100,200,300,50, and 50 bytes the sample for this editor would be . Furthermore, the byte count data was verified to be log-normal under the Shapiro–Wilk test for each treatment and bytes added metric and, given rejection of the null hypothesis (), t-tests were performed over the transformed data sets.
R Output
|
|---|
> pef1.bytes.added.process(pef_data_ba, c("bytes_added_net","bytes_added_pos","bytes_added_neg"))
[1] "Processing Metric bytes_added_net :"
[1] "Processing treatment control :"
[1] "Shapiro Test for control under bytes_added_net"
Shapiro-Wilk normality test
data: log(data_lst)
W = 0.9911, p-value = 7.511e-11
[1] "Sample Size: 2359"
[1] "Mean: 465.136210445125"
[1] "Log Mean: 4.66078657222061"
[1] "Log SD: 1.82530027988423"
[1] "Processing treatment experimental_1 :"
[1] "Shapiro Test for experimental_1 under bytes_added_net"
Shapiro-Wilk normality test
data: log(data_lst)
W = 0.9927, p-value = 2.805e-09
[1] "Sample Size: 2293"
[1] "Mean: 618.24601116769"
[1] "Log Mean: 4.81233905664943"
[1] "Log SD: 1.79442556781165"
[1] "Processing treatment experimental_2 :"
[1] "Shapiro Test for experimental_2 under bytes_added_net"
Shapiro-Wilk normality test
data: log(data_lst)
W = 0.9902, p-value = 2.652e-11
[1] "Sample Size: 2262"
[1] "Mean: 906.927550903443"
[1] "Log Mean: 4.77470093786469"
[1] "Log SD: 1.79614274486428"
[1] "T-test for treatment1 experimental_2 under bytes_added_net"
Welch Two Sample t-test
data: t1 and ctrl
t = 3.9262, df = 5691.451, p-value = 8.732e-05
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.09452417 0.28305084
sample estimates:
mean of x mean of y
4.849211 4.660424
[1] "T-test for treatment1 experimental_2 under bytes_added_net"
Welch Two Sample t-test
data: t2 and ctrl
t = 2.4333, df = 5639.082, p-value = 0.01499
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.02282736 0.21208532
sample estimates:
mean of x mean of y
4.777880 4.660424
Saving 7 x 7 in image
[1] "Processing Metric bytes_added_pos :"
[1] "Processing treatment control :"
[1] "Shapiro Test for control under bytes_added_pos"
Shapiro-Wilk normality test
data: log(data_lst)
W = 0.9918, p-value = 8.289e-11
[1] "Sample Size: 2552"
[1] "Mean: 453.809529561939"
[1] "Log Mean: 4.63171598380423"
[1] "Log SD: 1.82551596580964"
[1] "Processing treatment experimental_1 :"
[1] "Shapiro Test for experimental_1 under bytes_added_pos"
Shapiro-Wilk normality test
data: log(data_lst)
W = 0.9931, p-value = 2.021e-09
[1] "Sample Size: 2467"
[1] "Mean: 595.539647110775"
[1] "Log Mean: 4.76851079603585"
[1] "Log SD: 1.80839824038114"
[1] "Processing treatment experimental_2 :"
[1] "Shapiro Test for experimental_2 under bytes_added_pos"
Shapiro-Wilk normality test
data: log(data_lst)
W = 0.9903, p-value = 9.056e-12
[1] "Sample Size: 2447"
[1] "Mean: 869.705414970591"
[1] "Log Mean: 4.71290079703554"
[1] "Log SD: 1.84080525982407"
[1] "T-test for treatment1 experimental_2 under bytes_added_pos"
Welch Two Sample t-test
data: t1 and ctrl
t = 3.2163, df = 5688.894, p-value = 0.001306
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.0606125 0.2498299
sample estimates:
mean of x mean of y
4.800620 4.645399
[1] "T-test for treatment1 experimental_2 under bytes_added_pos"
Welch Two Sample t-test
data: t2 and ctrl
t = 1.4521, df = 5628.177, p-value = 0.1465
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.0247694 0.1663061
sample estimates:
mean of x mean of y
4.716168 4.645399
Saving 7 x 7 in image
[1] "Processing Metric bytes_added_neg :"
[1] "Processing treatment control :"
[1] "Shapiro Test for control under bytes_added_neg"
Shapiro-Wilk normality test
data: log(data_lst)
W = 0.9939, p-value = 0.0001134
[1] "Sample Size: 1148"
[1] "Mean: 342.283259605728"
[1] "Log Mean: 2.90049652487514"
[1] "Log SD: 2.30528787301969"
[1] "Processing treatment experimental_1 :"
[1] "Shapiro Test for experimental_1 under bytes_added_neg"
Shapiro-Wilk normality test
data: log(data_lst)
W = 0.9847, p-value = 2.122e-09
[1] "Sample Size: 1113"
[1] "Mean: 1512.99104330916"
[1] "Log Mean: 2.87175485686431"
[1] "Log SD: 2.347390161243"
[1] "Processing treatment experimental_2 :"
[1] "Shapiro Test for experimental_2 under bytes_added_neg"
Shapiro-Wilk normality test
data: log(data_lst)
W = 0.9917, p-value = 5.151e-06
[1] "Sample Size: 1140"
[1] "Mean: 416.417118019785"
[1] "Log Mean: 2.87935974123138"
[1] "Log SD: 2.29814679460416"
[1] "T-test for treatment1 experimental_2 under bytes_added_neg"
Welch Two Sample t-test
data: t1 and ctrl
t = -0.4148, df = 5682.92, p-value = 0.6783
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.14628784 0.09519063
sample estimates:
mean of x mean of y
2.847405 2.872953
[1] "T-test for treatment1 experimental_2 under bytes_added_neg"
Welch Two Sample t-test
data: t2 and ctrl
t = 0.2923, df = 5636.002, p-value = 0.7701
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.1020320 0.1377847
sample estimates:
mean of x mean of y
2.890830 2.872953
Saving 7 x 7 in image
|
| Type of Addition | Treatment | Sample Size | Mean | log(Mean) | log(SD) | Shapiro-Wilk Confidence | T-Test P-value against Control |
|---|---|---|---|---|---|---|---|
| Net | Control | 2359 | 465.136 | 4.66078657222061 | 1.825 | 7.511e-11 | -- |
| Net | Confirmation | 2293 | 618.246 | 4.81233905664943 | 1.794 | 2.805e-09 | 8.732e-05*** |
| Net | Gratitude | 2262 | 906.928 | 4.775 | 1.796 | 2.652e-11 | 0.01499* |
| Positive | Control | 2552 | 453.810 | 4.632 | 1.826 | 8.289e-11 | -- |
| Positive | Confirmation | 2467 | 595.540 | 4.769 | 1.808 | 2.021e-09 | 0.001306** |
| Positive | Gratitude | 2447 | 869.705 | 4.713 | 1.841 | 9.056e-12 | 0.1465 |
| Negative | Control | 1148 | -342.283 | -2.900 | 2.305 | 0.0001134 | -- |
| Negative | Confirmation | 1113 | -1512.991 | -2.872 | 2.347 | 2.122e-09 | 0.6783 |
| Negative | Gratitude | 1140 | -416.417 | -2.879 | 2.298 | 5.151e-06 | 0.7701 |
| Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 | |||||||

The results indicate that both treatments outperformed the control significantly for net byte count per edit. The confirmation condition significantly outperformed the control for positive byte count per edit, while we found a marginally significant effect for gratitude. No significant difference was observed on the negative byte count per edit (or content removal). Therefore, receiving feedback has an effect on the size of contributions compared to the content added by editors in the control condition.
Time to threshold[edit]
We measured the time to threshold as the number of minutes between the first and second edit. Only editors that came back to make a second edit were included in this analysis. Using this metric helps us address the following:
- RQ3. Does receiving feedback shorten the time to the second contribution?
R Output
|
|---|
[1] "Shapiro Test for control under time_diff" Shapiro-Wilk normality test data: data_lst W = 0.5458, p-value < 2.2e-16 [1] "Sample Size: 1669" [1] "Mean: 1349.33792690234" [1] "SD: 325.516585763998" Saving 7 x 7 in image [1] "Shapiro Test for experimental_1 under time_diff" Shapiro-Wilk normality test data: data_lst W = 0.5707, p-value < 2.2e-16 [1] "Sample Size: 1586" [1] "Mean: 1338.82408575032" [1] "SD: 342.104898333354" Saving 7 x 7 in image [1] "Shapiro Test for experimental_2 under time_diff" Shapiro-Wilk normality test data: data_lst W = 0.5082, p-value < 2.2e-16 [1] "Sample Size: 1624" [1] "Mean: 1344.52955665025" [1] "SD: 322.600064079319" [1] "T-test for treatment1 experimental_2 under time_diff" Welch Two Sample t-test data: data_frames[1]$x and data_frames[2]$x t = 0.8973, df = 3220.399, p-value = 0.3696 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -12.45908 33.48676 sample estimates: mean of x mean of y 1349.338 1338.824 [1] "T-test for treatment1 experimental_2 under time_diff" Welch Two Sample t-test data: data_frames[1]$x and data_frames[3]$x t = 0.4257, df = 3289.893, p-value = 0.6703 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -17.33703 26.95377 sample estimates: mean of x mean of y 1349.338 1344.530 |
The table below contains the mean values of time-to-threshold for each treatment where the
| Treatment | Sample Size | Mean | Standrad Deviation | Shapiro-Wilk Confidence | T-Test P-value against Control |
|---|---|---|---|---|---|
| Control | 1669 | 1349.338 | 325.517 | 2.2e-16 | -- |
| Confirmation | 1586 | 1338.824 | 342.105 | 2.2e-16 | 0.3696 |
| Gratitude | 1624 | 1344.530 | 322.600 | 2.2e-16 | 0.6703 |
| Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 | |||||
Observing the table above and the plots below it seems that there tends to be a clustering effect of making a second edit around one day later. The strength of this effect in itself is particularly interesting. However, there seems to be no significant effect on the basic response time as a result of the feedback provided.
Quality[edit]
While feedback may increase the volume of newcomer edits, it might do so at the cost of decreased quality. This is concerning since increasing the amount of edits that will need to be reverted is counter productive. Similarly increasing the amount of newcomers who eventually need to be blocked would increase the burden on en:WP:AIV.
To explore whether the changes in the volume of newcomer work were coming at the cost of decreased quality, we examined the work that newcomers performed in their first two weeks of editing. We identified two aspects of newcomers and the work that they perform: the proportion of newcomers who were eventually blocked from editing and the rate at which newcomers' contributions were rejected (reverted or deleted). We used these metrics to answer the following questions:
- RQ4. Does feedback affect the rate at which newcomers are blocked?
- RQ5. Does feedback affect the success rate of newcomers?
Block rate[edit]
To determine which newcomers were blocked, we processed the logging table of the enwiki database to look for block events for newcomers in the experimental conditions. We decided that a newcomer had been blocked if there was any event for them with log_type="block" AND log_action="block" between the beginning of the experimental period and midnight GMT Sept. 5th. Blocked newcomers plots the proportion of newcomers were blocked by experimental condition. As the plot suggests, the difference in proportions varies insignificantly (around 0.072) which suggests that the experimental treatment had no meaningful effect on the rate at which newcomers were blocked from editing.
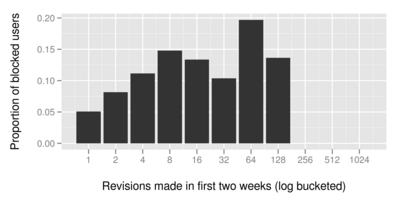
To make sure that this result wasn't due to blocks of editors who hadn't earned them through a series of bad-faith edits, we examined the relationship between the number of edits these newcomers saved and the proportion of them that were blocked. Blocked newcomers by revisions shows a steady increase in the proportion of newcomers that were blocked between 1 and 4 revisions. This seems likely due to the 4 levels of warnings that are used on the English Wikipedia. Based on this, we subsampled for only those newcomers who edited at least 4 times in their first two weeks (n = 2726). As expected Blocked active newcomers shows an increase in the proportion of blocked newcomers across all experimental conditions, but the figure also suggests an insignificant effect of the experimental treatments and the proportion of these active newcomers who were blocked.

Success rate[edit]
We examined the en:SHA1 checksum associated with the content of revisions to determine which revisions were reverted (see Research:Revert detection) by other editors. By comparing the number of revisions saved with the number of revisions reverted, we can build a proportion of reverted revisions (see Research:Metrics/revert_rate) and the success rate (the proportion of revisions saved by an editor that were not reverted). We use the success rate of an editor as a proxy for the quality of their work and a direct measure of the additional work their activities necessitate from Wikipedians.
To look for evidence of a causal relationship between PEF and the quality of newcomer work, we calculated the mean success rate for newcomer for each experimental condition. Newcomer success rate (overall) does not show a significant difference between either of the experimental conditions and the control. Instead, overall success rate appears to vary insignificantly around 0.775. This result suggests that the experimental treatment had no meaningful effect on the overall quality of newcomer contributions, and therefore, the burden imposed on Wikipedians.
However, reverting behavior is strange outside of the main namespace, where encyclopedia articles are edited. Newcomers success rate (articles) plots the mean success rate for article edits. Again the figure suggests no significant differences between the experimental conditions and the control.
We also worried that blocked users may add noise to this measure since those users presumably came to Wikipedia in bad faith and would have a low success rate regardless of any intervention. Newcomers success rare (articles, no blocks) again shows an insignificant difference between the experimental conditions which suggests that PEF has no measurable effect on the success rate of newcomers.